Spherical Dense Packing

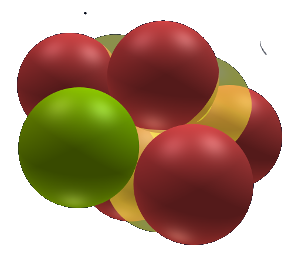
In SAM, the nucleus is constructed by putting protons (positive charge) together in a geometrical structure with electrons (negative charge). The inner electrons (of yet unknown form and size) are located inside this structure at very specific positions, acting as a sort of “glue.”

A single sphere exists by itself.

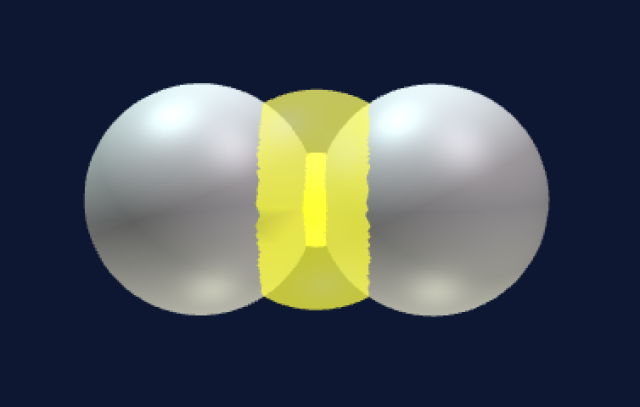
Two spheres can attach to each other in only one way (i.e., next to each other.

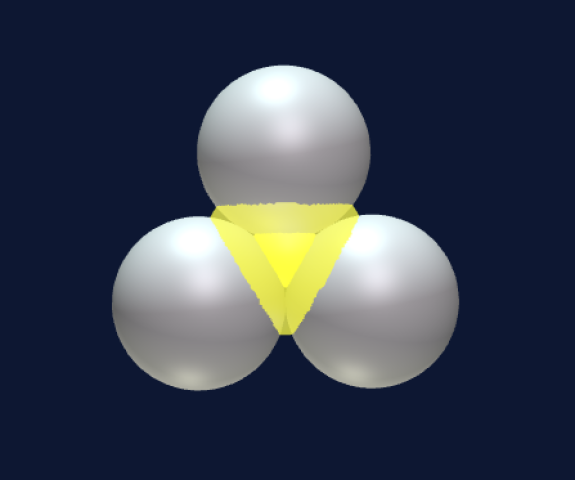
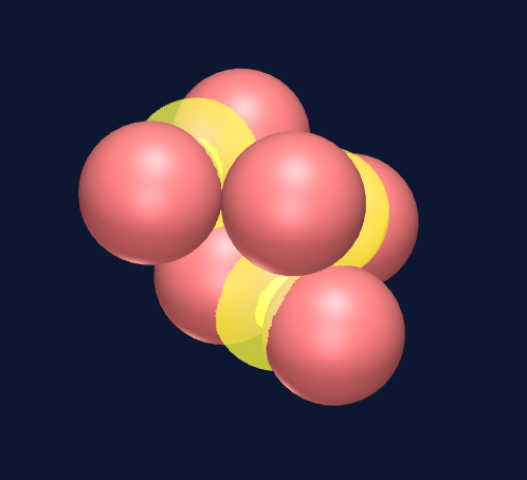
With three spheres there are two possibilities—in a line or in a triangular shape.

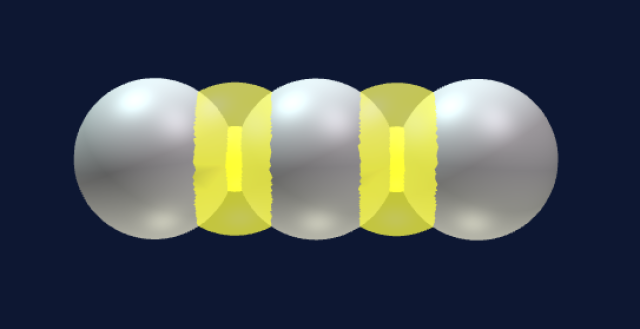
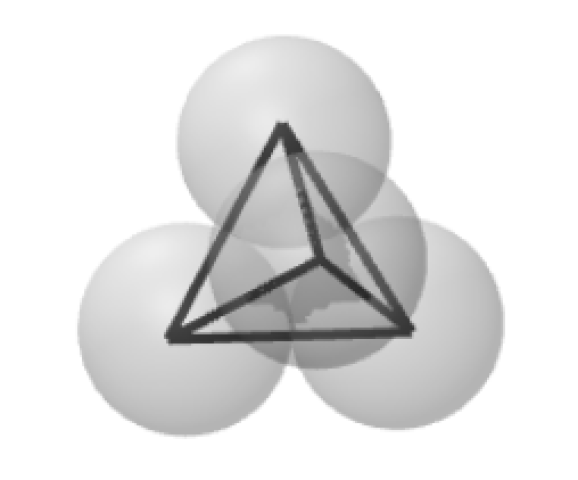
The position of the inner electron in the triangular case is a research topic. Does it stay with the deuteron or does it move to the middle of the structure? Four spheres have three possibilities—all four in a line, in the shape of a square, and in the shape of the tetrahedron.

Four in a line doesn't work because it is not a spherically dense structure, neither is the square. We are left with the tetrahedron.

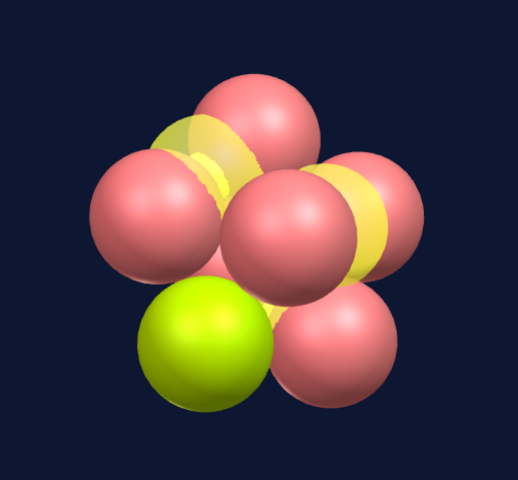
The fifth sphere cannot be added without distorting the structure of the tetrahedron, with the inward-pulling force breaking it. There is no stable structure with five spheres. The spheres push each other out of a dense structure and create distortions in the structural shape—there is no final resting shape for clusters of five spheres. Not unexpectedly, there does not exist a stable isotope of an element with five nucleons.

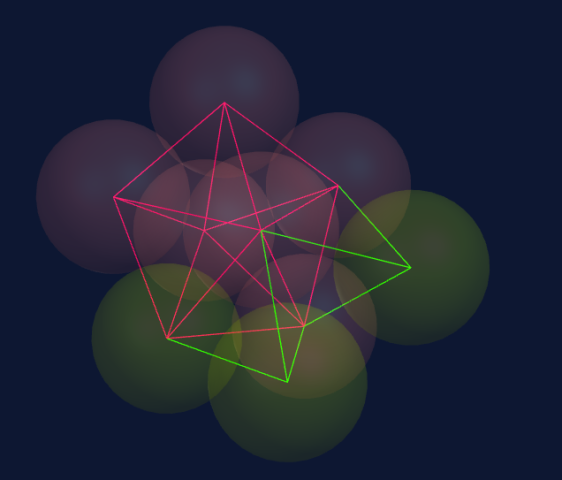
Six spheres create an octahedron, and at first glance this appears to be stable and densely packed.

However, since the spheres are being pulled toward a common center, opposite spheres will push apart the four connected protons and instead create a five-sphere ring structure with an additional sphere on one side at the center of the ring.

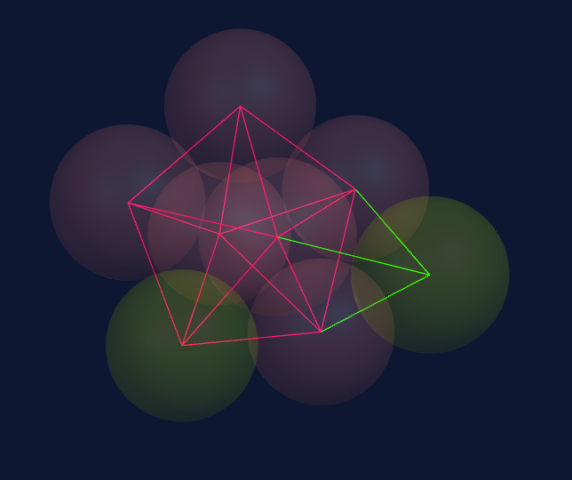
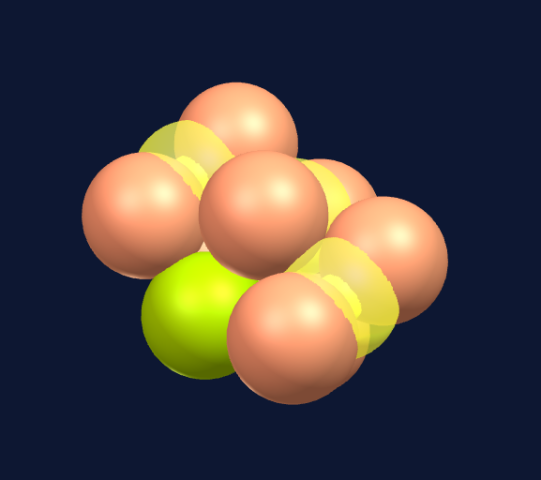
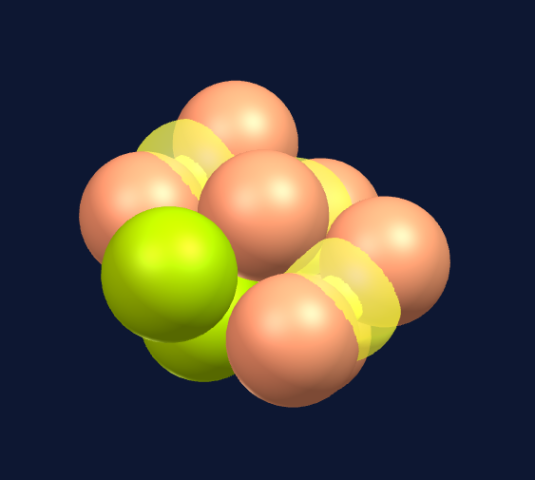
Seven spheres come together to form a pentagonal bi-pyramid consisting of a ring of five spheres and a top and bottom sphere to cap the ring.

Eight spheres create the same conditions found with five spheres. The inward-pulling force causes the 8th sphere to penetrate the ring below it, breaking the underlying structure. It is not possible to create a stable structure that is densely packed with eight spheres. And again, as with five nucleons, there exists no stable isotope of an element with eight nucleons. We consider this to be an important confirmation of spherical dense packing as a principle of nucleon organization.

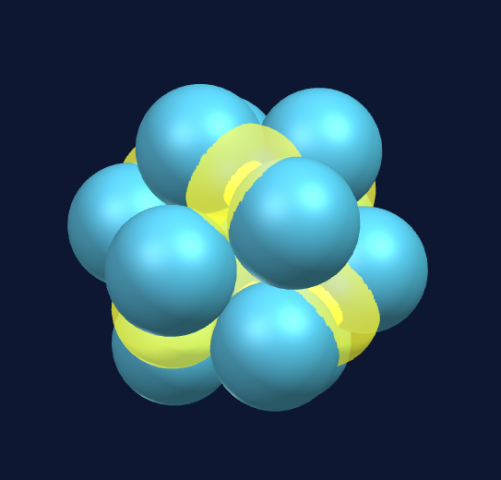
When adding two spheres on top of the pentagonal bi-pyramid (seven spheres), we create two new tetrahedrons, each combining with three spheres in the structure.

These tetrahedrons are stronger than the underlying structure and modify it accordingly; therefore, the underlying structure is not destroyed.

The 10th sphere creates the next viable structure.

The different colors signify repeating structural patterns, not material difference, all are protons.

The 11th sphere completes the next tetrahedron structure.

The 12th sphere creates a structure with an icosahedron shape, via an intermediary step—the largest platonic solid that can be densely packed and is perfectly symmetrical.

This is a very stable structure. Even though it follows the rules for spherical dense packing toward a common center it is hollow on the inside.